Lesson 15 - Dose equivalence
In this lesson we translate the physical dosimetric concepts learned in the previous
lesson into the biological effects that we are usually called upon to quantify. (I
say "usually" with an eye toward our previous widely-defined concept of
"detector" -- some of our "detectors" are NOT biological, e.g.,
detector response, total flux, TLD readings, etc.)
Relative Biological Effectiveness
The direct translation of absorbed dose into biological effect can be obtained using a
"reverse method" of measuring the ratio of the type and severity of a given
biological effect (e.g., genetic damage, onset of leukemia, etc.) due to a given dose of
some given particle at some given energy to the effect of the same dose of a reference
particle. The reference particle is usually 250 keV photons (or, more precisely, an
x-ray source with this peak energy spectrum)..
Example: If a dose of 10 rad of 5 MeV neutrons produces a 10
times greater incidence of leukemia in a controlled population than 10 rads of the
reference 0.25 MeV photons, the "leukemia RBE" for 5 MeV neutrons would be 10.
Note that:
- RBE differs for (a) different types of particle, (b) different energies for the same
type of particle, and (c) different biological effects being examined.
- Despite this detail of dependence, it DOES NOT depend on the dose level itself. In
our above example, we would take the results and ASSUME that 20 rad of 5 MeV neutrons
would produce 10 times the leukemia incidence of 20 rads of the reference photons.
This might not be true.
Quality Factor, Q
For regular health physics work, the idea of RBE is simplified to a so-called quality
factor, Q, that is used the same way as RBE (i.e., a relative measure of biological effect
for different types and energies of particles) with the following characteristics:
- The biological effects of interest by which quality factors are defined are set to be
the long-term health effects of cancer incidence and/or genetic effects of radiation.
This concentrates our concern on the most commonly measured (and worried about)
health effects of occupational exposure and accidental public exposure.
- Rather than depend on direct "rad vs. rad" biological effect measurements, the
quality factor is defined for a given charged particle as depending on the linear energy
transfer (LET) in water, which we learned earlier was a measure of how quickly a particle
loses energy as it slows down. The common unit for LET is keV/micrometer.
- There are two "flavors" of LET (finite and infinite) based on whether all
of the energy loss of a charged particle is considered imparted to the material in its
path (
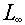 ) or whether a lesser
amount is considered imparted to the material in its path because of fact that delta rays
(i.e., high energy secondary electrons) carry away some of the energy to be imparted some
distance from the path ( ) or whether a lesser
amount is considered imparted to the material in its path because of fact that delta rays
(i.e., high energy secondary electrons) carry away some of the energy to be imparted some
distance from the path (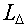 ,
where the ,
where the 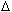 is a
distance). In this notation, the subscript concerns the distance from the path that
is considered to be "on" the path. The Q value is defined using is a
distance). In this notation, the subscript concerns the distance from the path that
is considered to be "on" the path. The Q value is defined using 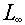 , imparting all of the energy lost
by the particle to the particles path. , imparting all of the energy lost
by the particle to the particles path.
Note: Tables 5.1 and 5.2 give two translations from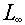 to Q that have been
proposed. Most of the response functions that you will encounter (at least for the
next few years) are based on Table 5.1 to Q that have been
proposed. Most of the response functions that you will encounter (at least for the
next few years) are based on Table 5.1
- For primary (i.e., uncharged) particles, we go with an average quality factor,
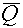 , which is based on a
dose-averaging of the quality factors of the secondary charged particles and scattered
primary particles. For example, if a neutron interaction produces 5 secondary
particles (including the recoil nucleus), each one of which has an associated absorbed
dose, , which is based on a
dose-averaging of the quality factors of the secondary charged particles and scattered
primary particles. For example, if a neutron interaction produces 5 secondary
particles (including the recoil nucleus), each one of which has an associated absorbed
dose, 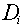 , and quality factor, , and quality factor, 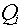 , the equation for the average
quality factor would be: , the equation for the average
quality factor would be:
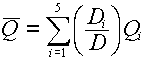
where D is the total dose, given by:
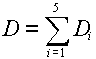
Example: The text makes an interesting statement when it says that
"The ICRP has suggested that for electrons a quality factor of unity may be used for
all energies, regardless of what the table might seem to require." Let's use
our Chapter 3 charged particle slowing-down experience to see what the table might
"seem to require" for electron energies of 1, 10 and 100 MeV in water of density
1 g/cc.
Answer: Using the quadratic fits from Table 3.6, we would get
ranges for electrons of:
1 MeV ==> 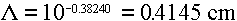
10 MeV ==> 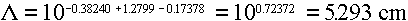
100 MeV ==> 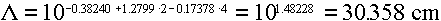
These would translate into 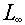 values of 0.24, 0.19, and 0.33, well within the Q=1 range from both Table 5.1 and Table
5.2.
values of 0.24, 0.19, and 0.33, well within the Q=1 range from both Table 5.1 and Table
5.2.
Dose Equivalence
The unit for dose equivalence is the Sievert (Sv); the common symbol is H. The
equation for dose equivalence is::
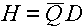
H will be in units of Sievert if D is in units of Gray (Gy). 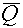 is, of course, dimensionless, but
don't be fooled by this fact into thinking that the Sievert is somehow "equal"
to the Gray; the two units measure different things (i.e., relative biological effect vs.
deposited energy), so should not be confused. is, of course, dimensionless, but
don't be fooled by this fact into thinking that the Sievert is somehow "equal"
to the Gray; the two units measure different things (i.e., relative biological effect vs.
deposited energy), so should not be confused.
In the "other" units, H will be in rem ("Roentgen
equivalent man" is how I learned it) if D is in rad.
|
 NE406
Radiation Protection and Shielding
NE406
Radiation Protection and Shielding